Problem description
According to the given picture which contains one written number among 0 to 9, It can recognize the number in the picture.
Ex) The picture below is the size of 28*28, which has 784 pixels. Each pixel contains information of location and the brightness.
By combining this two information, the picture is determined what number it is. Forwawrd and back propagation are used when the model is made.
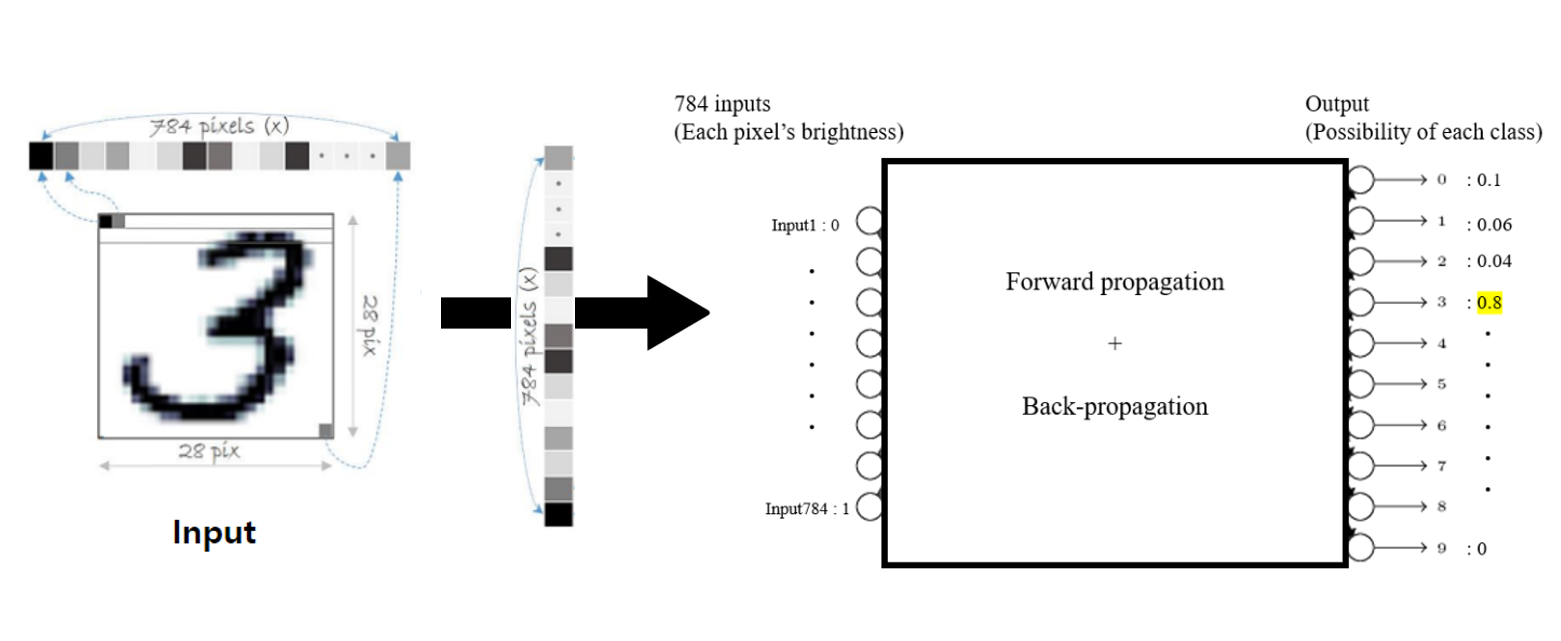
Forward propagation
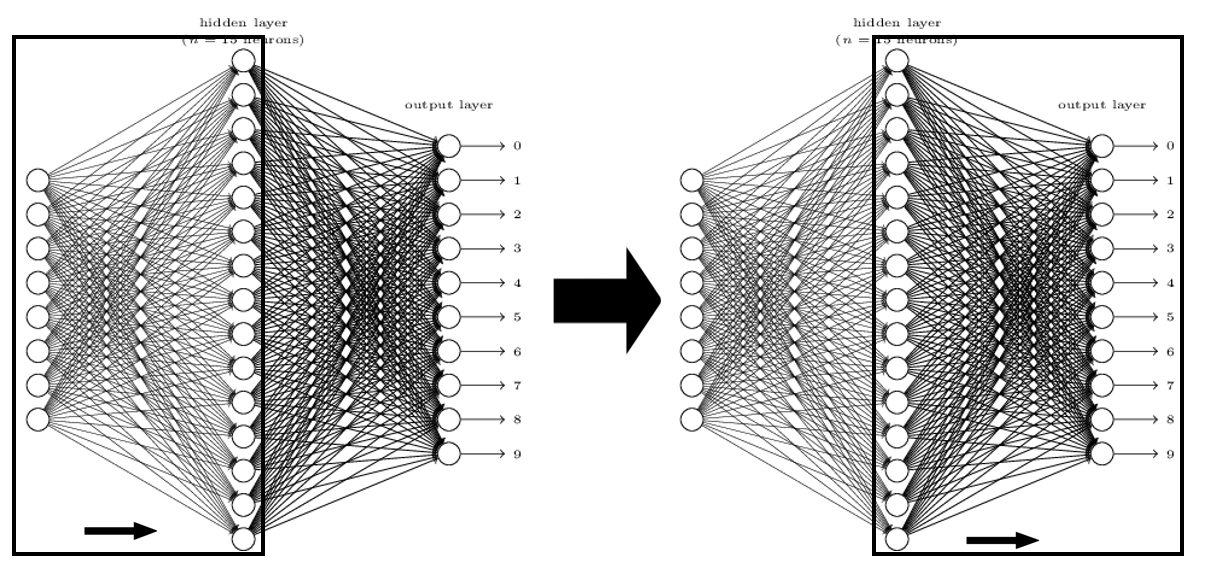
Forward propagation is inferring the value using a model created based on input values and answer.
Each node in the neural network is called perceptron.
Input perceptrons affect perceptrons in the next layer, and this perceptrons in the next layer affects perceptrons in its next layer.
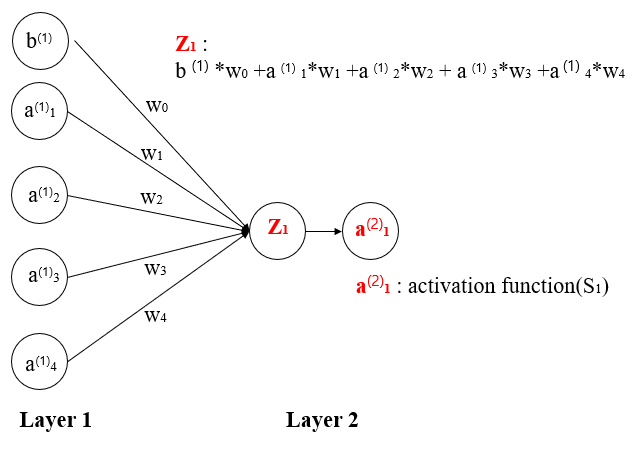Each perceptrons in the input layer are used to make perceptron in the next layer. The values of each perceptron are multiplied by weights and is summed up to make perceptrons in the next layer.
The result of summation then becomes the input of activation function such as sigmoid, ReLu, and softmax (only at the last layer, in classification problems).
Creating a right model is largely related to finding right weights. Input values are given, therefore by changing weights, proper model can be made.
Evaluating errors strategy depends on whether it is a regression model or a classification model. Usually, a regression model uses sigmoid function, and a classification model uses ReLU and sigmoid function.
Since what we are doing in this project is a classification model problem, we will look about how to back propagate ANN that uses ReLU and SoftMax function.
Firstly, let us think about how we can find proper weights. It can be done by evaluating errors of a current model, and changing its weights based on errors.
With Back propagation.
However, we cannot find proper weights at one go. The initial weights are randomized and then it slowly changes over time.
In classification problems, the last output is driven by cross-entropy and SoftMax function.
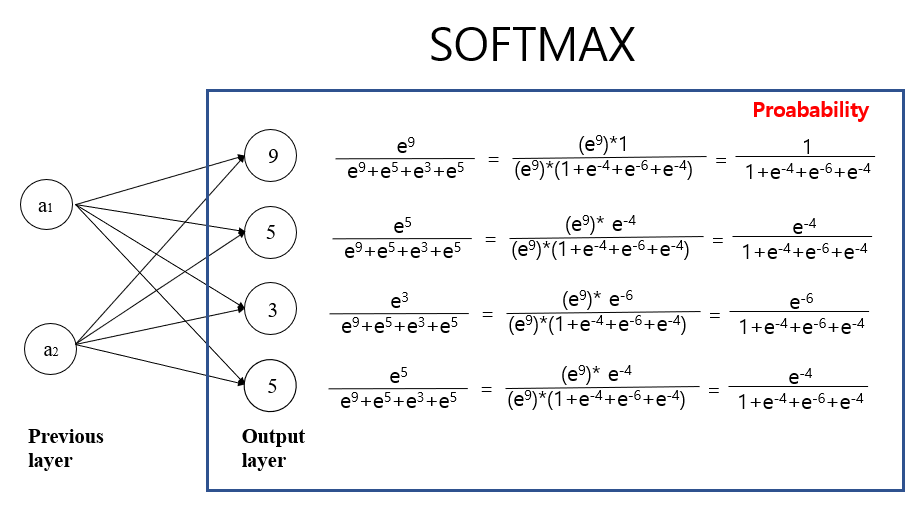
Let's assume that we have 4 classes(A,B,C,D), and each outcome is 9, 5, 3, 5 respectively (These outcome comes from the formula such as a1*w1 + a2*w2 + bias)
What we need to do is simply pick a class with the largest number, which means 'the strongest signal'. A(9) in this case.
Let's slightly change the format as probability. (Easier to deal with because its lower and upper bound is set.)If we can change it as probability like down below, and the result stays the same.
(Roughly rounded)
A : 9/(9+5+3+5) = 0.4
B : 5/(9+5+3+5) = 0.23
C : 3/(9+5+3+5) = 0.14
D : 5(9+5+3+5) = 0.23
But here not only probablity form but also Euler's number to present the probability for each class.
(The reason for using Euler's number is closely related to the back propagation (makes easier to differentiate), and the cross entropy error function.)
Now, (e9 + e5 + e3 + e5) is the denominator for each class, and the numerator is e9 , e5 , e3 , e5 for each class.
A : e9/(e9 + e5 + e3 + e5) = 0.96
B : e5/(e9 + e5 + e3 + e5)= 0.017
C : e3/(e9 + e5 + e3 + e5) = 0.0023
D : e5/(e9 + e5 + e3 + e5) = 0.017
y= ex is a monotone increasing function, so It does not change the magnitude of the relation.
(At the end of the day, our purpose is to pick up the class with the highest probability)
However, again problem when the number gets too big to be handled on computer.
Modificiation like down below can be a good solution.
A:9 B:5 C:3 D:5 .
First, find the biggiest number which is 9(A) and then subtract 9 for all classes.
A: 0 B:-4 C:-6 D:-4
A : e0/(e0 + e-4 + e-6 + e-4) = 0.96
B : e-4/(e0 + e-4 + e-6 + e-4) = 0.017
C : e-6/(e0 + e-4 + e-6 + e-4) = 0.0023
D : e-4/(e0 + e-4 + e-6 + e-4) = 0.017
(The probability is still the same.)
Conclusion
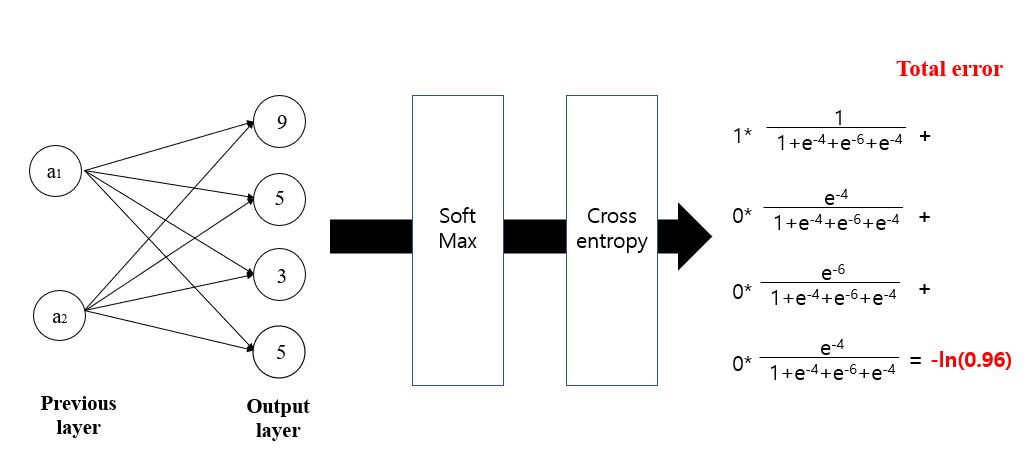
outcome -- softmax function --> probability
We first need to know how much errors the model has. To evaluate this error, Crossentropy function is often used (in classification problems.)
After using softmax function, we could convert each number into possibility of each class.
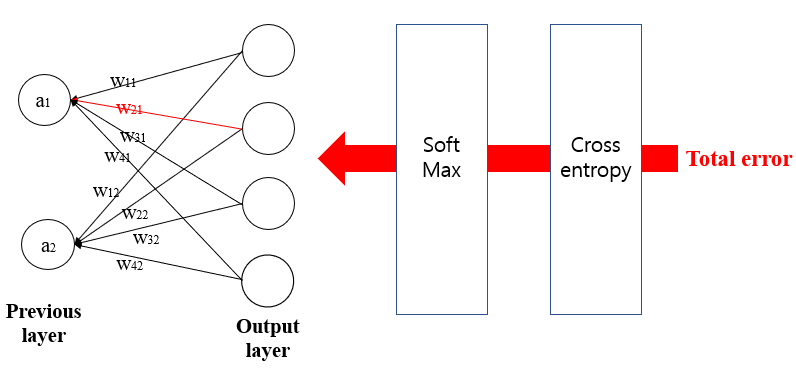
Now, let's assume this picture belongs to class A. This model was close, as the outcome was 0.96 for class A.
However, if the picture belongs to class B, then this model is significantly wrong because the possibility of belonging in class B is only 0.017.
The error is calculated by multiplying two numbers, - ln(The possility of beloning in each class) * Correct answer, and summed up.
If the estimation is close enough, then it will get lower costs. if it is not close, then the loss will be high.
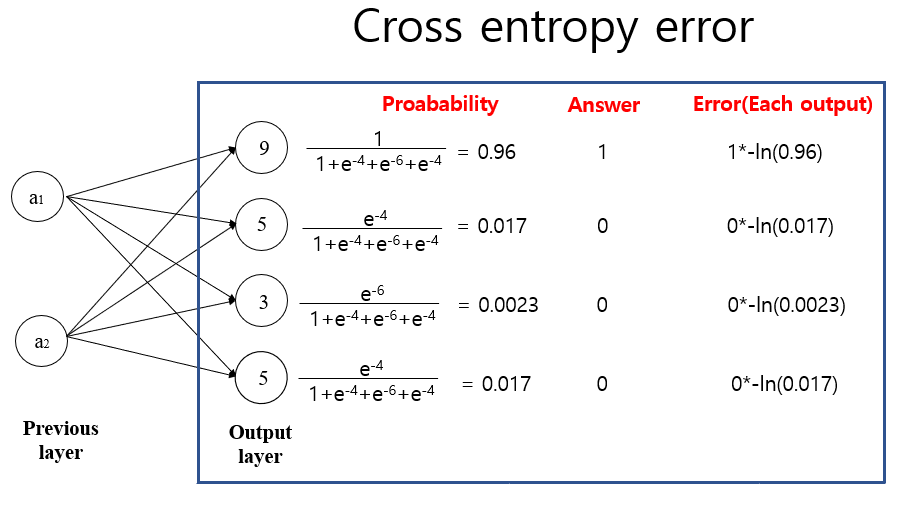
let's assume correct answer is (A,B,C,D)= (1,0,0,0)
Then,
cost for A = 1*(-ln(0.96+0.002)) = 1*(0.0406)= 0.0406 . so, the cost is very low.
cost for B,C,D = 0*(-ln(...))= 0 (So, In cross entropy error, we only care about how close the correct answer is with estimation, don't care about how correct(wrong) is for BCD.))
If, the probability of A was not 0.96 but 0, then?
Cost for A = 1*(-ln(0+0.002)) = 1*(6.2146)= 6.2146 . so the cost is very high compared to previous one.
also, this is reason why we should add small numbers like 0.002, because -ln0 is infinite.
(Click more to read) When the last output was from the sigmoid function
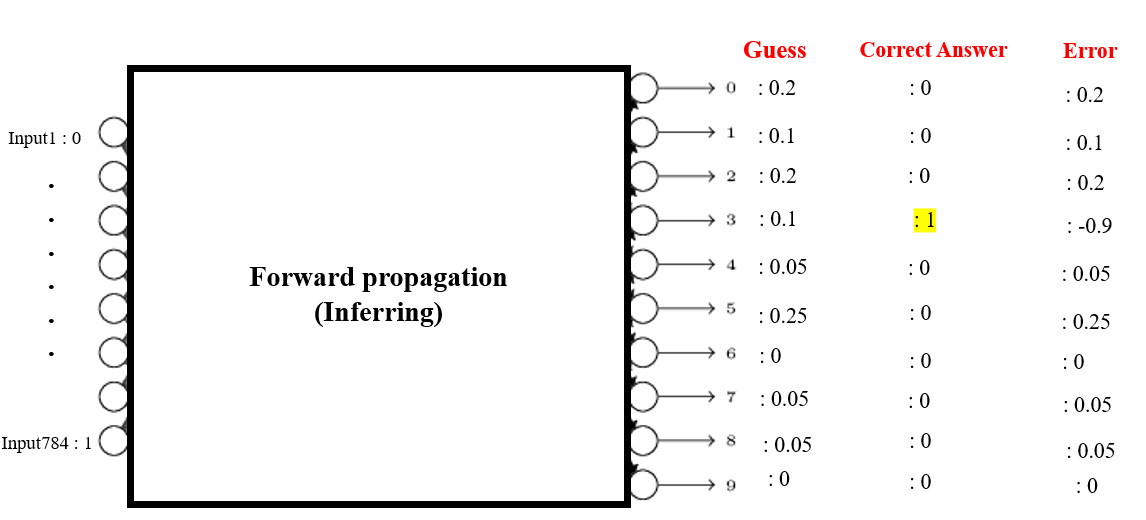
How do we know how much errors we have in this model?
If we simply add the errors?
0.2+0.1+0.2+(-0.9)+(0.05)+0.25+0+0.05+0.05+0 = 0.5 +(-0.9) +0.3 =
-0.01
the errors is only -0.01. It is becuase some nodes have different sign, so they cancel out each other's errors.
To avoid this, squaring each errors and then add.
0.2
2+0.1
2+0.2
2+(-0.9)
2+(0.05)
2+0.25
2+0
2+0.05
2+0.05
2+0
2=
1.01
The evaluation function we will use here is 1/2(correct answer-estimated answer)
2
(1/2)*1.01 = 0.505
error for this case
Back-propagation
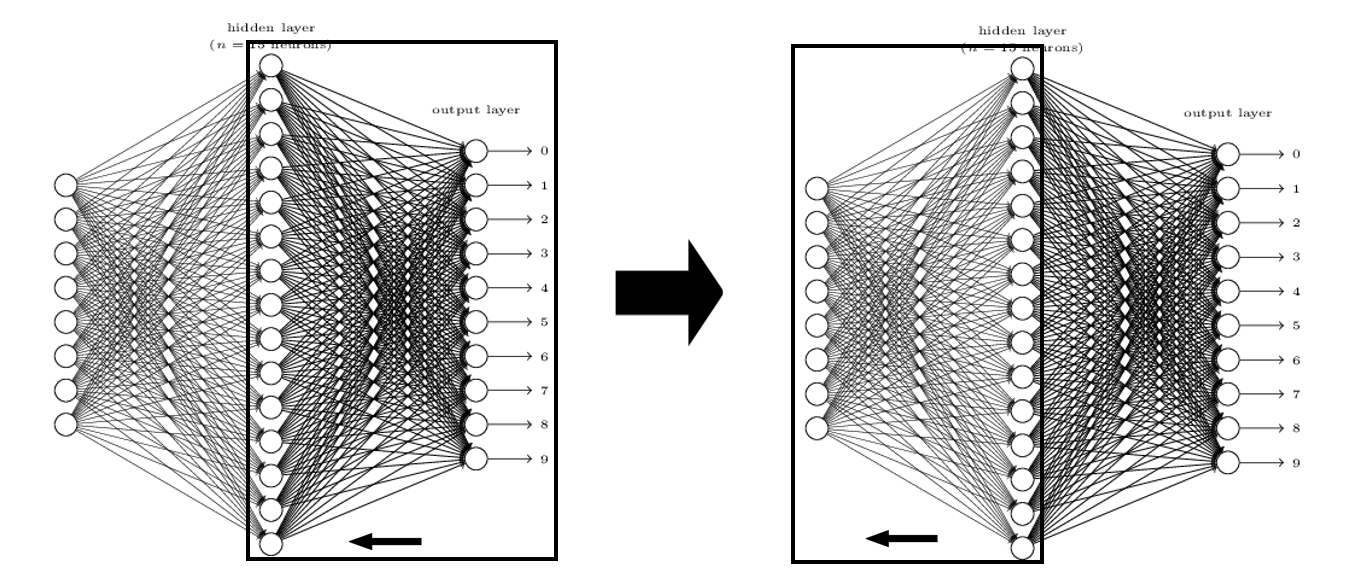
Back-propagation is the process of neural network finding right weights. Depending on how much each node contributes to the total error.
we will focus on 1. How much error each node contributes 2. How much weight should be updated
Back-propagation starts from the nodes from the output layer. These nodes can be evaluated by seeing how different it is from the right answer
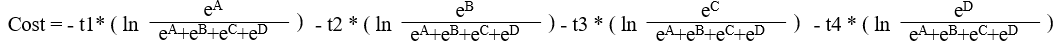
Even we do not explicitly see w11 from the equation above, cost function contains w11, as the A contains w11.
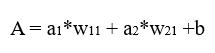
Therefore, we can differentiate the cost function with respective to w11(Weights).
The equation below is showing the differentiation of the cost function. It also means the moment slope, and derivatives.
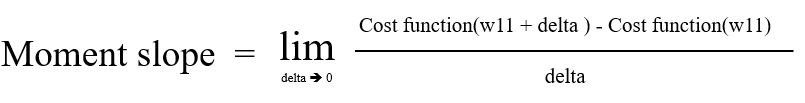
purpose is to minimize 'y' value, since y stands for the costs (total errors of all nodes)
If the moment slope is positive, it means when w11 goes to positive side, cost increases. If the moment slope is negative, then when w11 goes to positive side, cost decreases.
The former case, w11 should go to negative side and the latter case, w11 should go to positive side to decrease overall cost.
Now, Let's elaborate on how to update weights. let us assume specific situation.
There are 4 classes as output, and let's name it class 1, 2,3 and 4 from the top to the bottom.
The picture belongs to class 1, so the correct answer for each class is 1,0,0,0 respectively.
we can simplify it as the equation below, since only one is multiplied by 1, and others by 0.
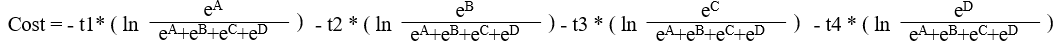
First, we will update w11. To update w11, we first need to calculate the derivatives. It can be done by following the chain rule.
-(1- A's probability) *a1 is the result of d(cost)/d(w11). If the derivative(moment slope) is positive value, then we need to go to the opposite direction of the value of derivatives to reduce the cost, and if it is negative value, also we need to go to the opposite direction of the value of derivatives.
Either way, it needs to head the opposite direction of the value of derivatives.
so,w11 +(1- A's probability)*a1. It is not complete formula, because we need to multiply appropriate small number called alpha(0.001 ,0.1...) to prevent to miss or skip the point we want to find.
w11 -alpha*((A's probability-1)*a1).
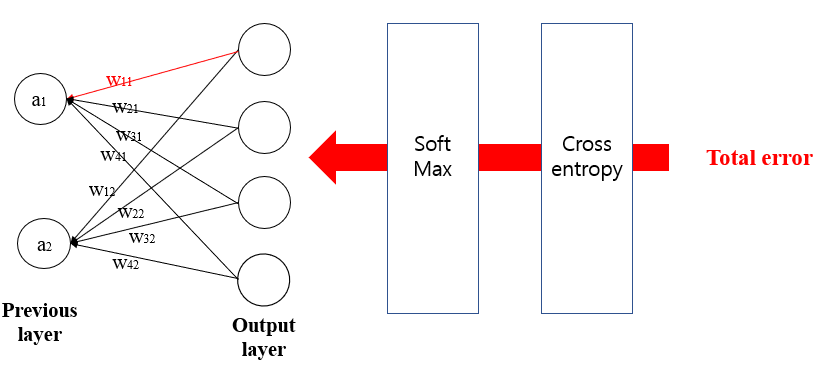
Now, let's update w21.It is similar but different since the cost function contains w21 only at the denominator. (It is different with updating w11, since the cost function contains w11 at the numerator and also at the denominator).
So differentiation result is different.
(B's probability-0)*a2 is the result of d(cost)/d(w21). So, the weight update would be w21 +alpha*(B's probability*a2).
By these two cases, we can generalize the way of updating weights.
weight - alpha*(probability- correct answer) *the previous output
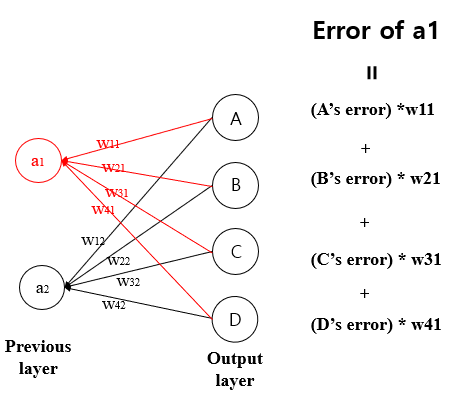
we can think (probability- correct answer) as an error of the output node. Now, to change the weights of the previous layer, we need to know the error of the previous layer's node.
Calculation is simple, the right picture below.
This is a basic pattern of machine learning. There are some more contents such as how to initialize good weights, (Xavier, He), regularization, and dropout.
these contents will be updated in the future.
