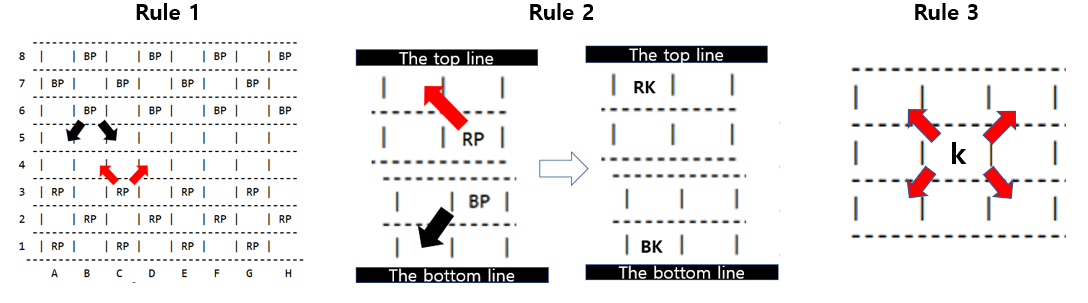
This project focused on making AI which can play against human by using mini max tree algorithm. Checkers is used for demonstrating the algorithm. The following is the rules of modified Checkers.
To decide, an appropriate indicator is needed to show the status of winning and losing. Indicator here is a score. Score is represented as only one number, zero sum, if black is winning then positive number will be shown, if res, then negative number. if it is tie, then it will be 0.
In this algorithm, zero sum is used. Score is expressed in one score, if Black is winning then score gets positive value, if not, score gets negative one. If it is equals, then score is 0.
(my method) If black pawn moves forward, then add 3. If red, subtract 3 from the total score. King worth 30 points. All pawns have a initial value of 10.

Let's elaborate the situation. Let's say the picture down below is current board, and now, red should make a decision. It has 7 different choice to make. Which choice is the best? Would it be all good choices?
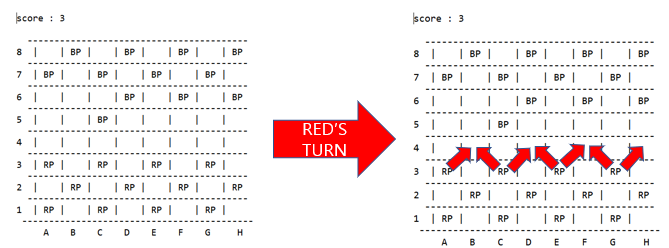
As you can think, two movements which is marked as a black are bad decision to make. The reason why is that, as soon as you move this forward, the opponent will get your pawn and get points.
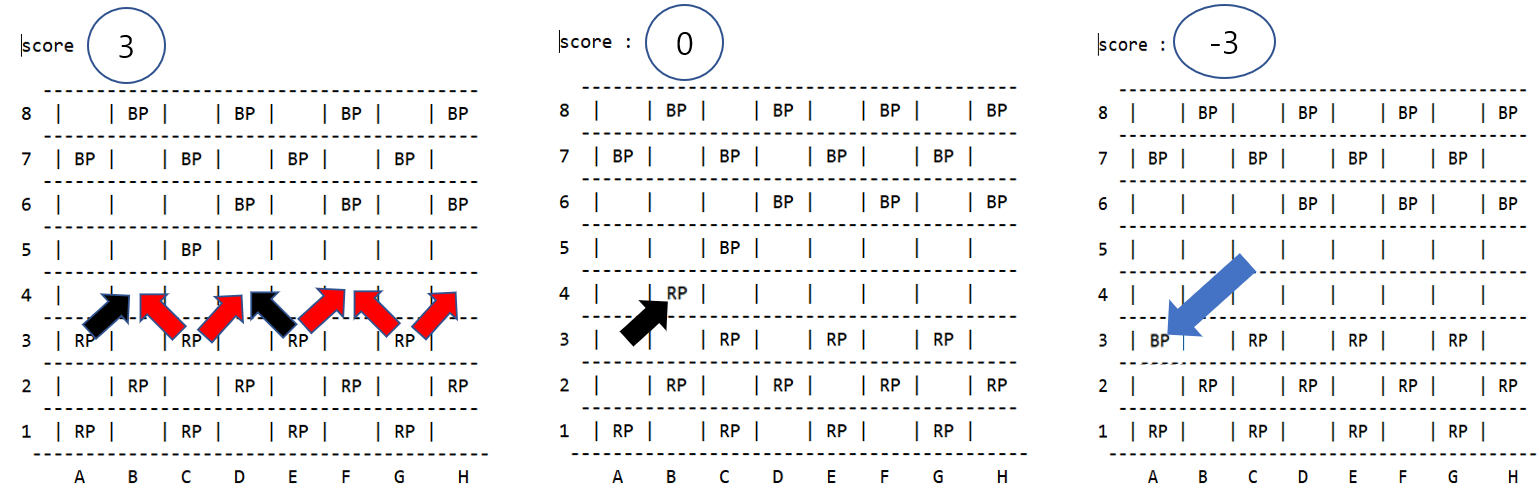
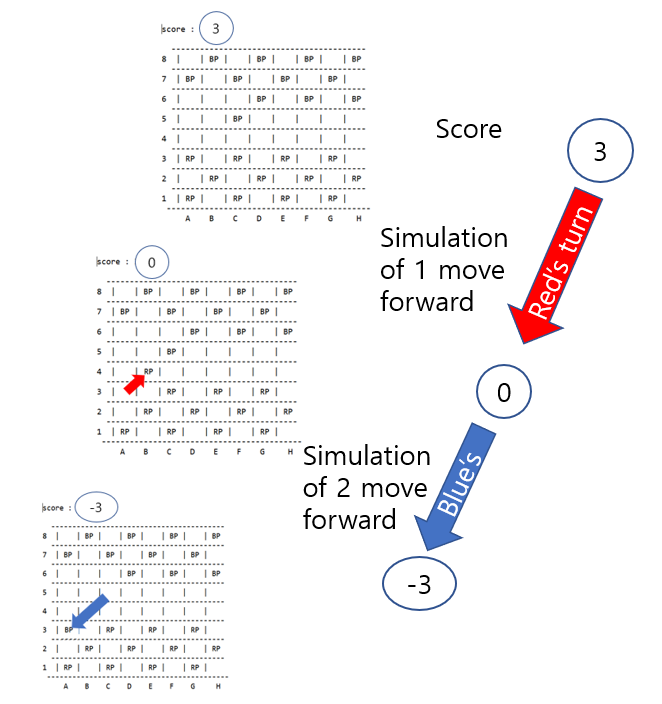
We can think of this as a tree form. Also, each situation is represented by the score.
depth 0 represents the current situation,
depth 1 represents one move forward from the current situation,
depth 2 represents two moves forward from the current situation.
If we complete the tree, it will be like the tree down below.
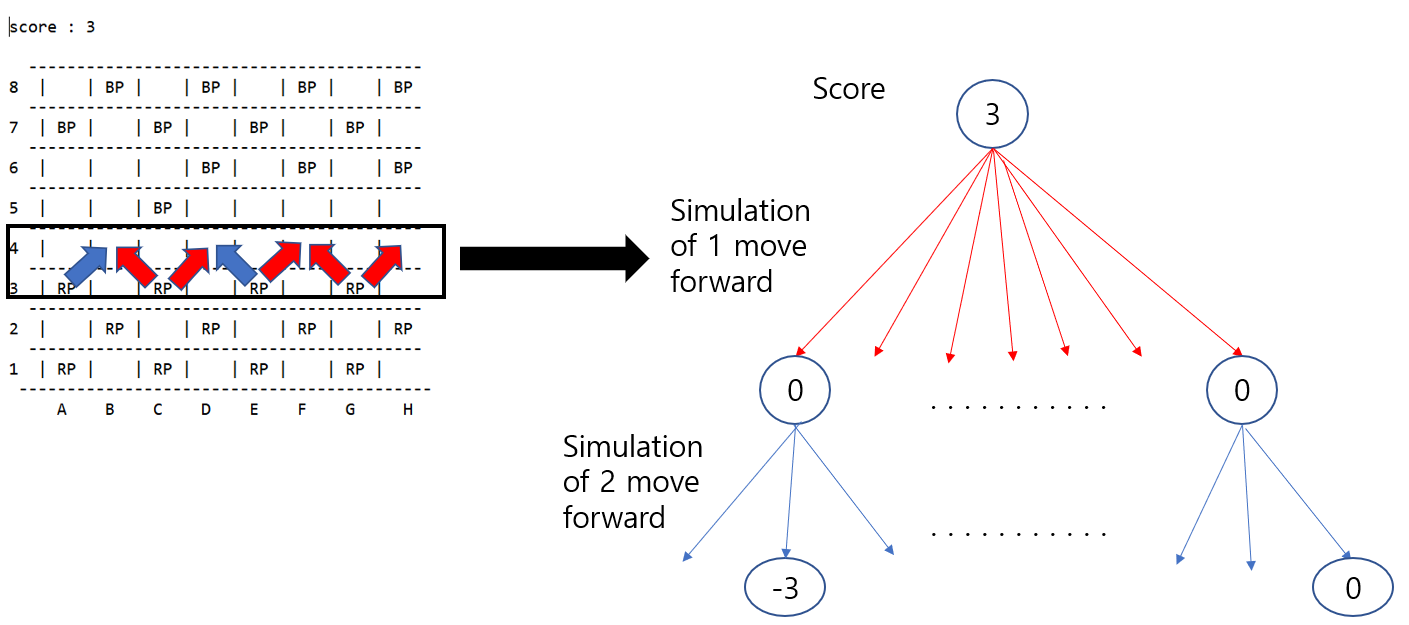
From here, we can think about a strategy that can lead us to make a good decision. Generate all the possible situation, and then evaluate. Let's say we consider the 2 moves forward from the current situation,2ply. (Usually even number ply is used because it considers the opponent's move). It is called "mini max tree"
* mini-max tree
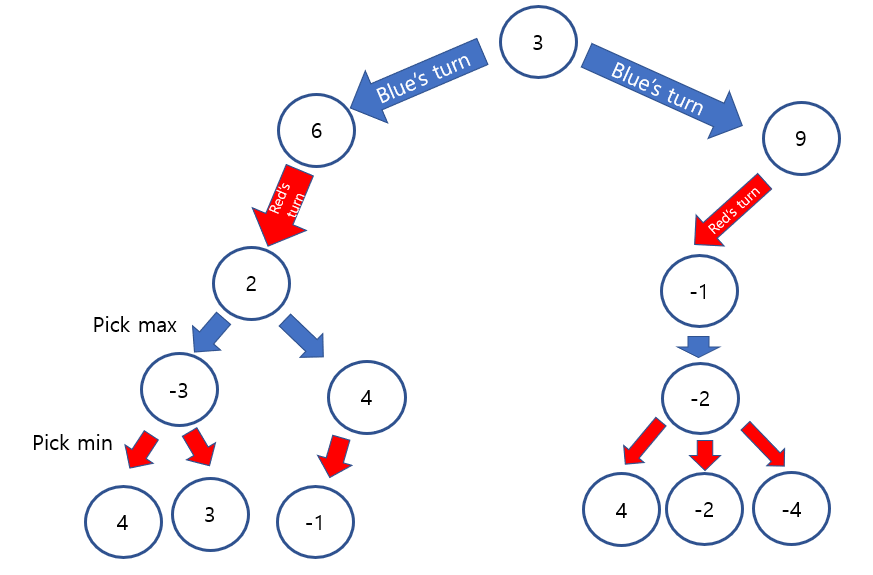
Now, let's make a decision in real. we are team blue, and we will consider 2 moves forward. + score means blue is winning, - score means red is winning. We need to pick one that brings us the optimal score.
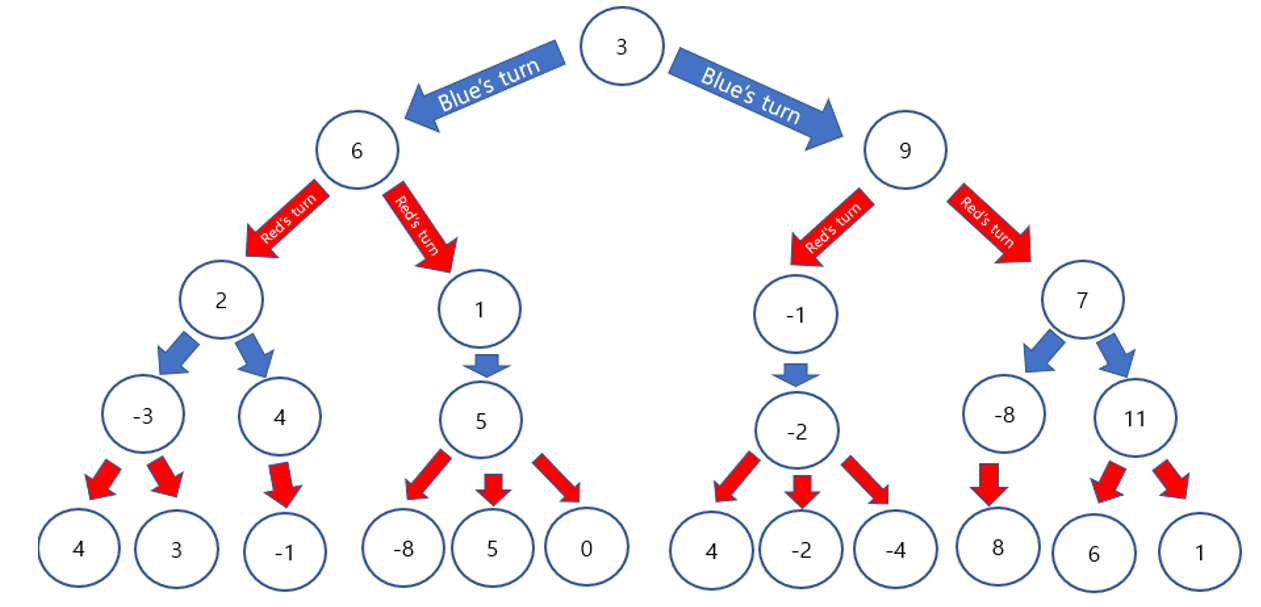
First, pick a smaller node among sister nodes at the depth 4(leaf), because since it is red's turn, it will pick the smallest value. After that, replace its parent's value as the value we pick.
Second, pick a bigger node among sister nodes at the depth 3(leaf), because since it is blue's turn, it will pick the biggest value. After that, replace its parent's value as the value we pick.
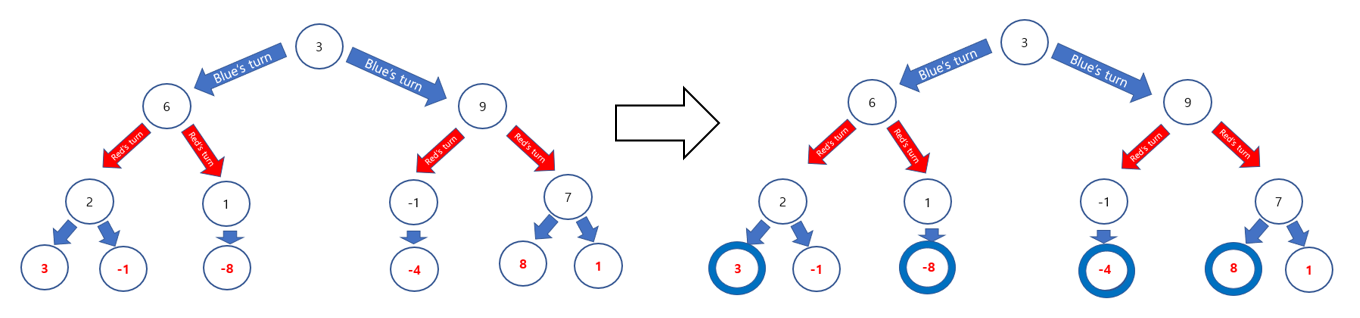
Second, pick a bigger node among sister nodes at the depth 3(leaf), because since it is blue's turn, it will pick the biggest value. After that, replace its parent's value as the value we pick.
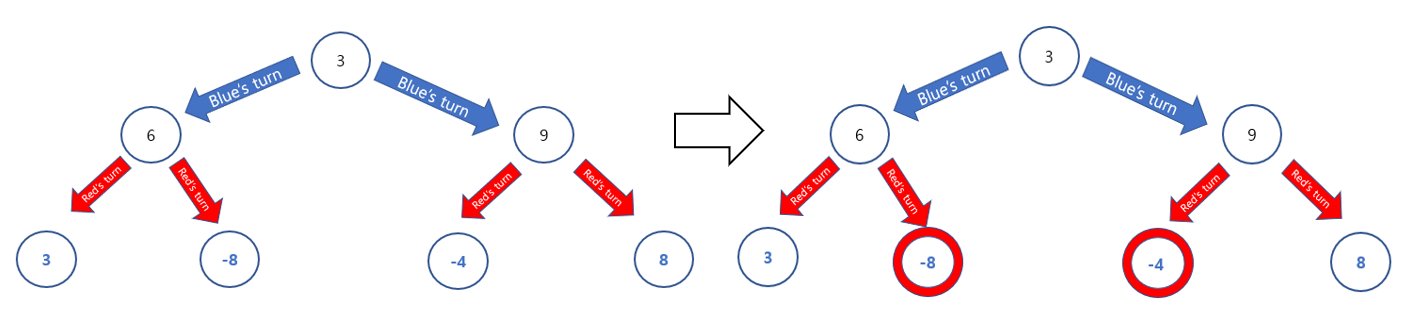
Repeaet this process until it gets the root.

Now, we can see which node we should pick to make optimal score. Two moves from now, the best score for us is -4.
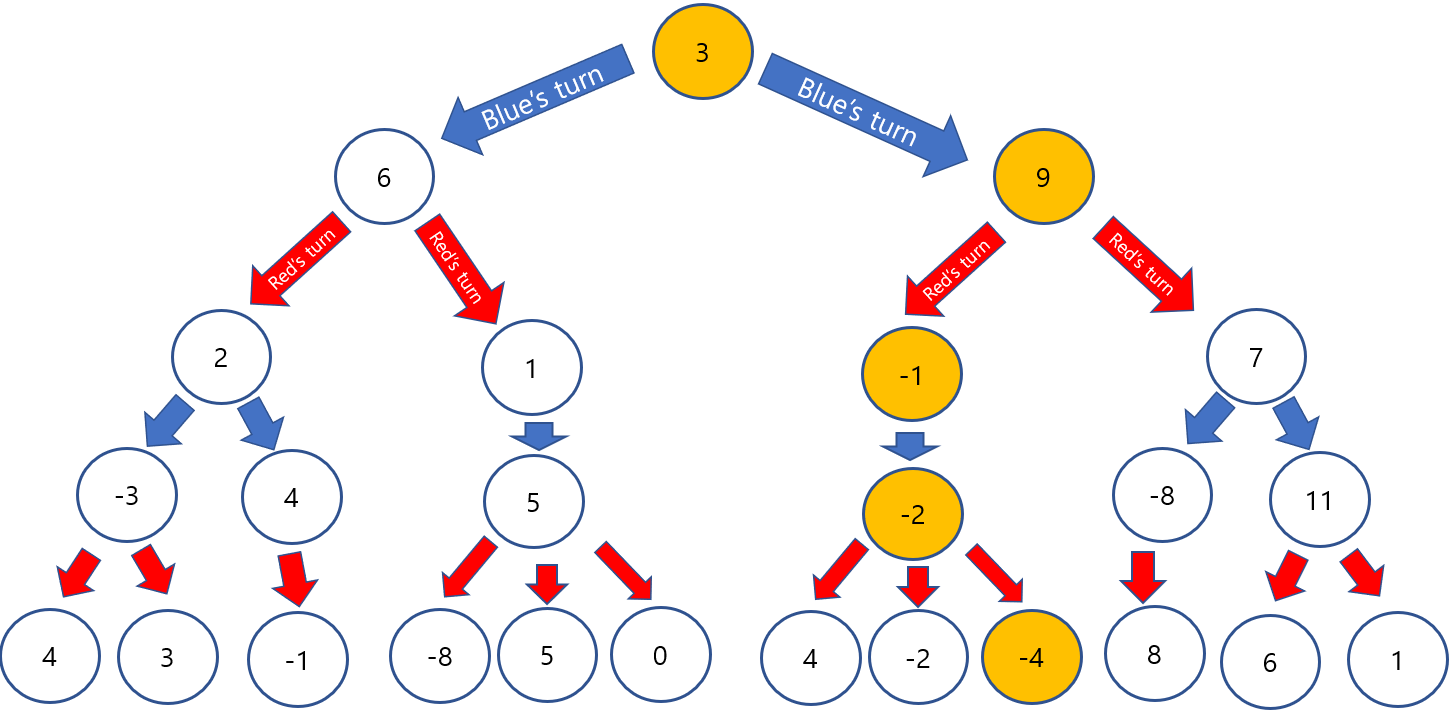
*alpha beta pruning*
Generating all the possibilities causes time and memory inefficiency. To solve this problem, alpha beta pruning is used.
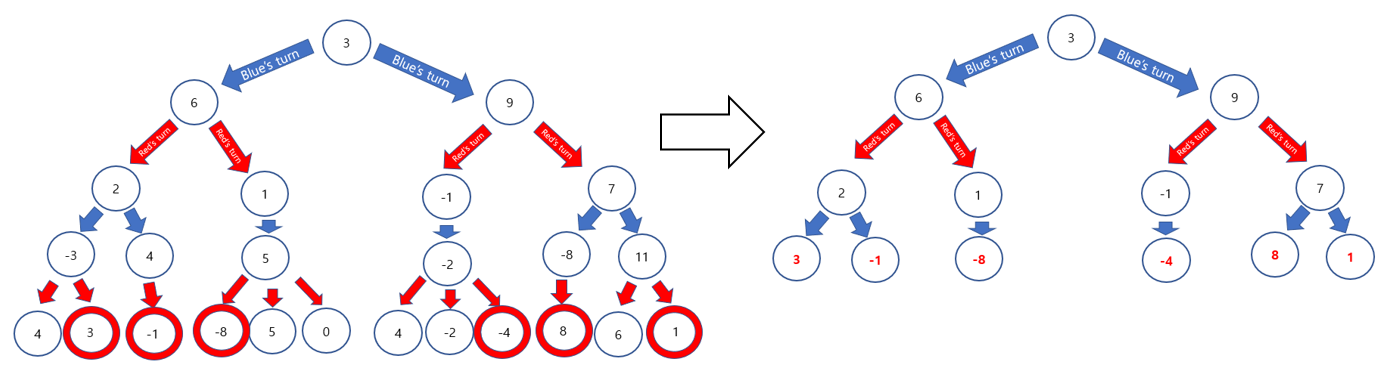
Firstly, pick the minimum value among sister nodes at depth 4, which is 3.
The temporal max value is 3. Now, we need to pick the smallest nodes again at depth 4.
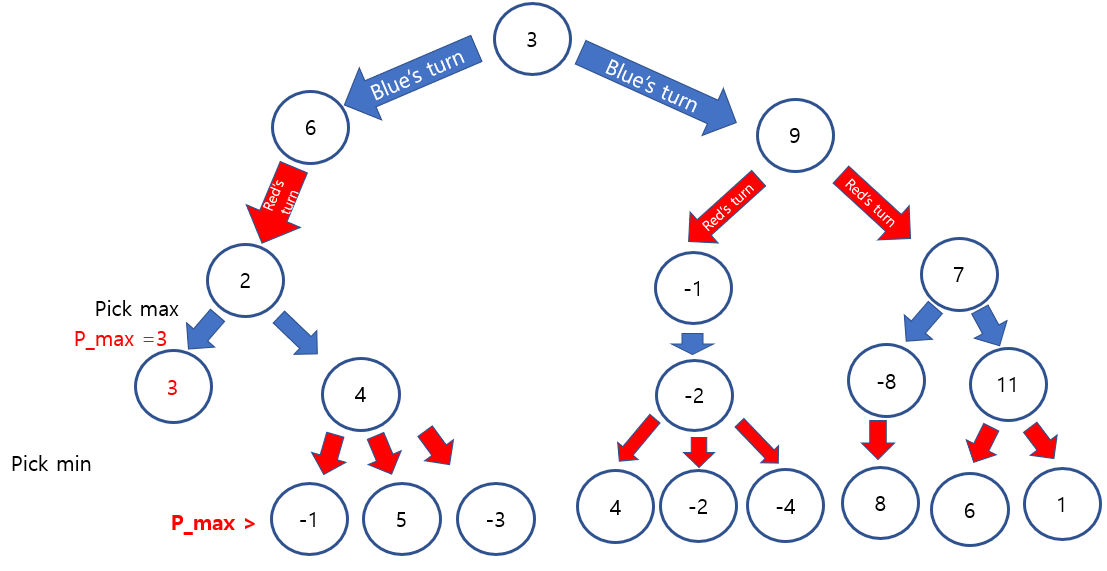
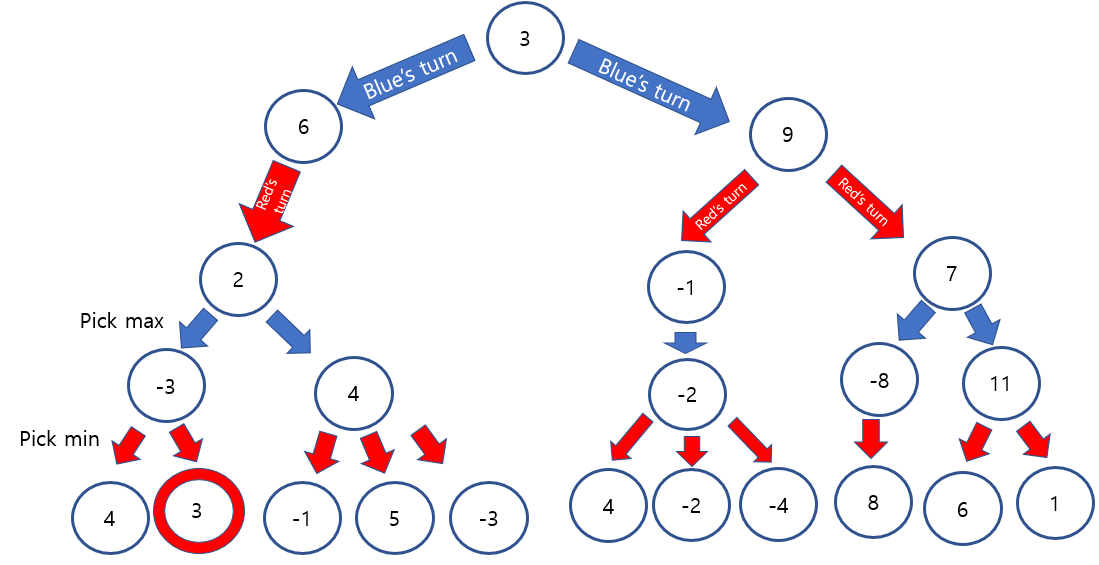
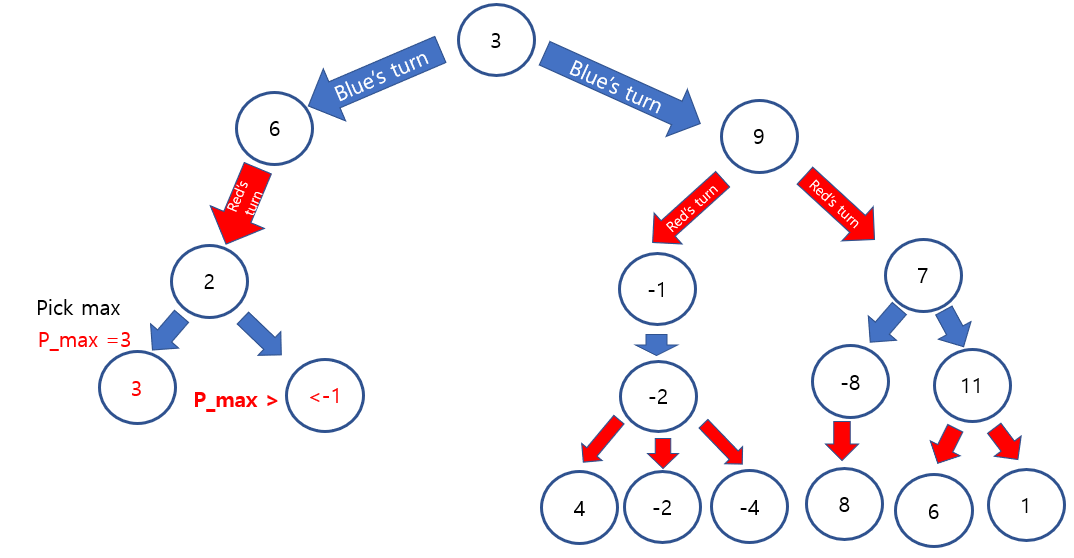
However, -1 is less than temporal maximum,3. the sister node of 3 would be less than -1, since the smallest node will be picked.
Therefore, we do not need to see other leaf nodes and can prune it.
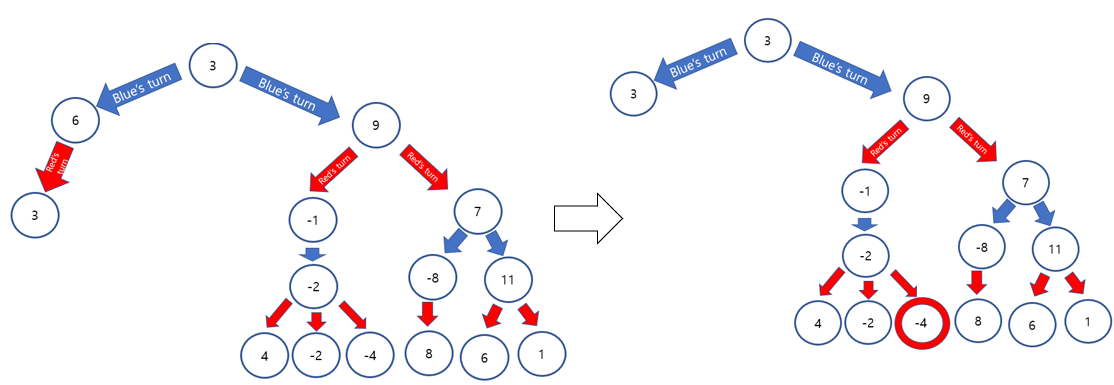
Now, pick the smallest one from the right side's leaf nodes. it is -4.
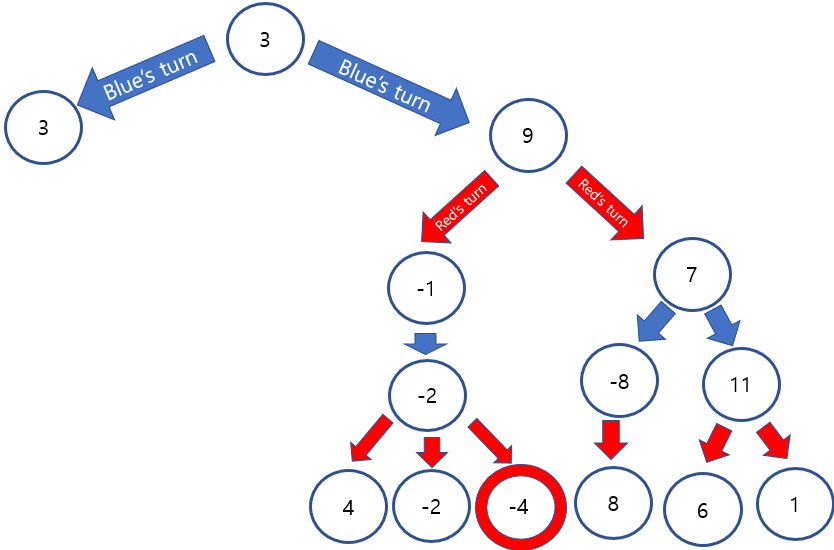
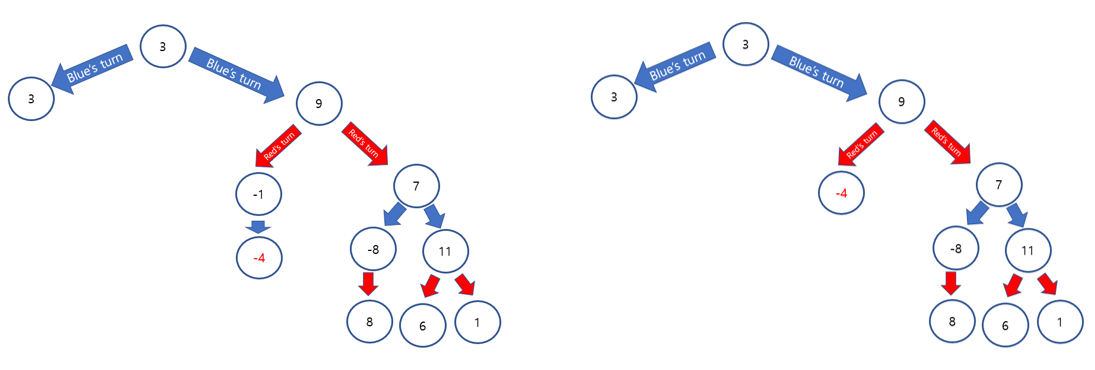
Temporal minimum is -4 at the right side of tree, depth 2. However, 3 is going to be always bigger than -4. blue will pick the value 3, left side, regardless of the values of right side of tree.
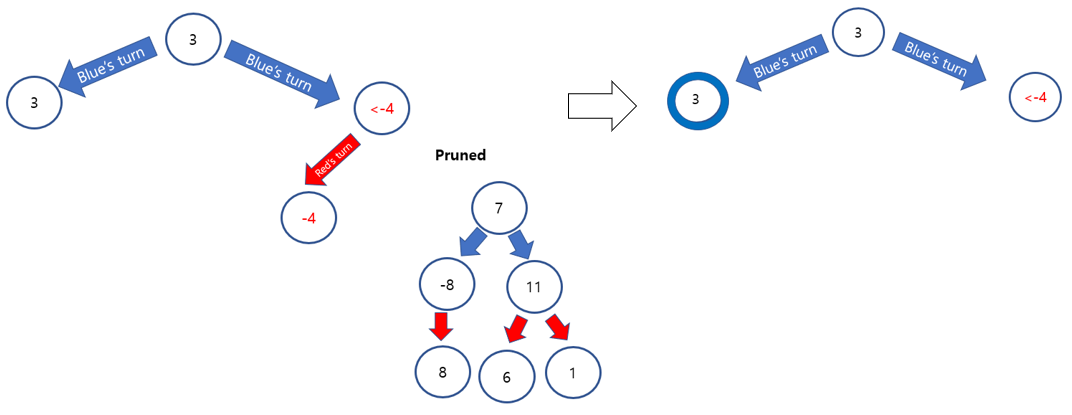
As a result, two points will be pruned.
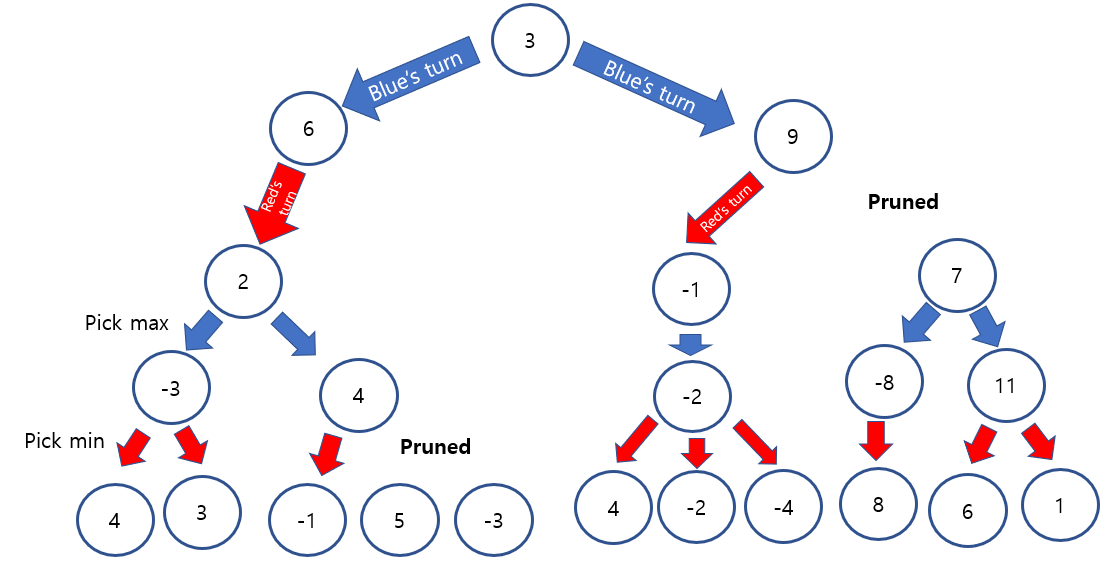
Therfore, alpha beta pruning can efficiently lessen the search space.